Recommend System Lecture Note(3)
July 2021 (271 Words, 2 Minutes)
3주차 강의의 key word 는 아래와 같다.
- 모델 기반 협업 필터링
- Latent Factor Model & SVD
- Matrix Factorization
- BPR Optimization with MF
- Annoy
3-1. Latent Factor Model & SVD
Latent Factor Model
Latent Factor Model는 유저와 아이템을 벡터로 압축하여 잠재 요인으로 표현하는 모델이다. 유저와 아이템을 여러 차원의 벡터로 나타내어 각각의 유사도를 확인할 수 있다.
Single Value Decomposition(SVD)
Rating Matrix R에 대해 유저와 아이템의 어떤 matrix로 분해한다.
Truncated SVD는 대표값으로 사용되는 k개의 특이값만 사용한다.

하지만 SVD는 분해하는 matrix의 정보가 불완전하면 정의될 수 없기에 entry를 모두 채우는 imputation을 적용한다. 이는 데이터를 왜곡시키고 계산량을 증가시키는 단점이 있다.
3-2. Matrix Factorization
MF는 user matrix, item matrix 2개로 이루어진다.
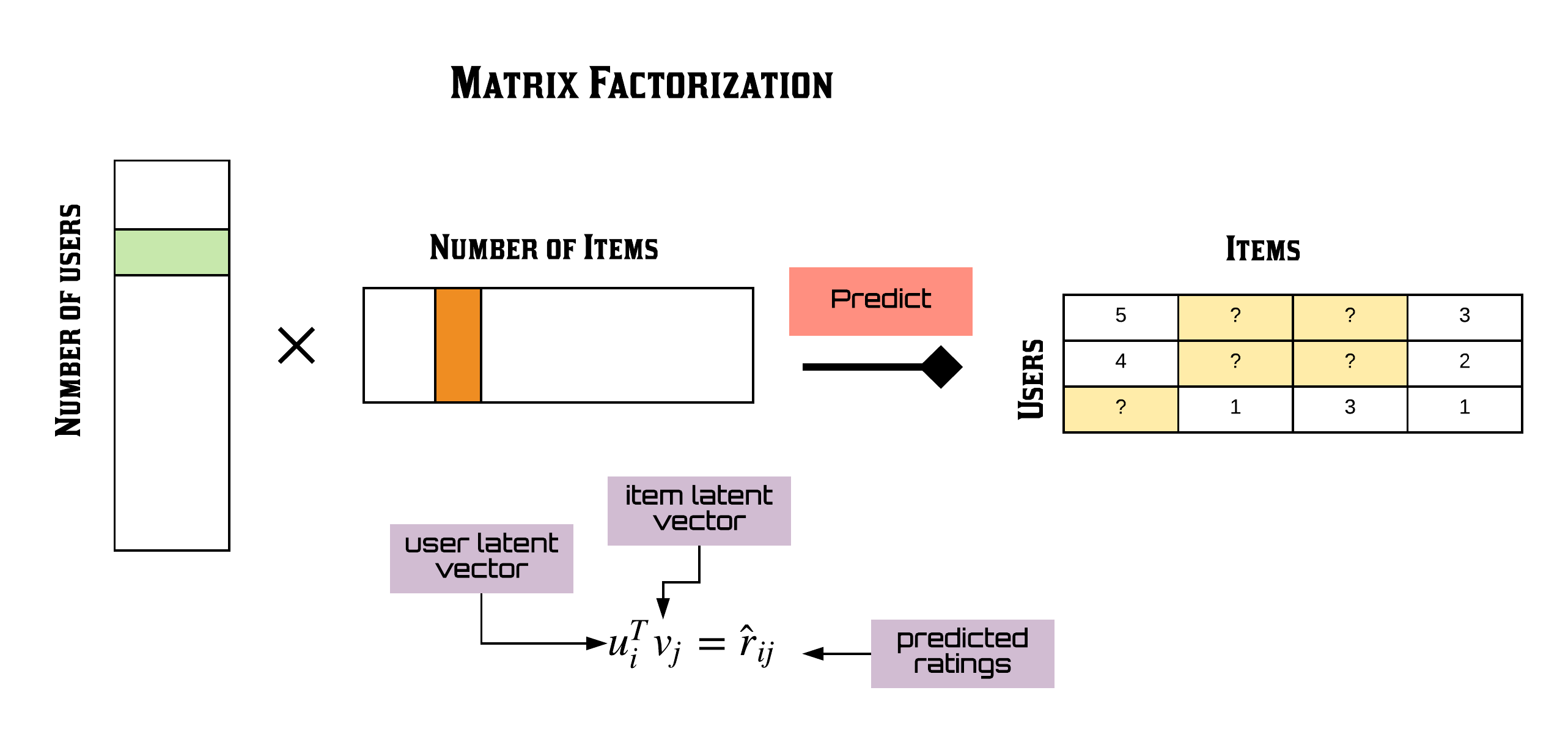
참고할 논문 : https://datajobs.com/data-science-repo/Recommender-Systems-%5bNetflix%5d.pdf
Stochastic Gradient Descent
Rating matrix의 objective는 실제 R matrix와 예측치가 최대한 유사하도록 loss를 줄이는 것이다. 학습방식은 stochastic gradient descent에 따라 weight를 업데이트하는 과정에 따른다.
SVD와 다르게 실측 데이터만을 대상으로 하여 결측치를 채워줄 필요가 없다. 람다를 넣어 L2 정규화를 포함시켜 weight를 조정하여 오버피팅을 방지한다.
SGD에 따라 파라미터를 업데이트한다.

Biases 추가
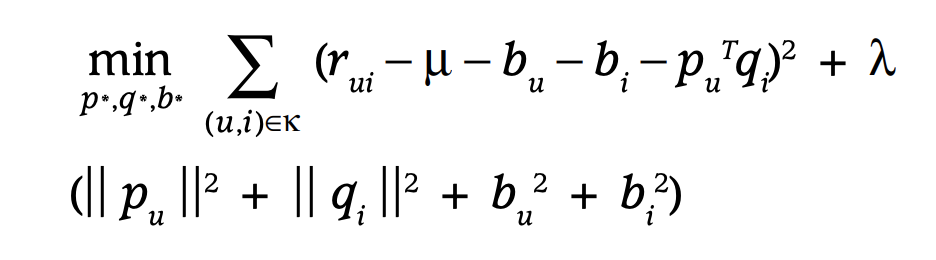
유저마다 평점을 매기는 기준이 상대적이기에 편향이 생길 수 있어 전체 평균 및 유저 - 아이템 bias를 추가하여 아래와 같이 파라미터를 업데이트한다.

참고할 논문: http://yifanhu.net/PUB/cf.pdf
Alternative Least Square
user / item matrix를 번갈아가며 업데이트한다. P은 고정하여 Q를 업데이트하거나 Q를 고정하여 P를 업데이트하는 방식을 반복한다.

Implict Feedback을 처리하는데 있어 Preference를 적용하여 유저가 아이템을 선호하는지 여부를 binary(0 or 1)로 표현하거나 Confidence를 적용하여 유저가 아이템을 얼마나 선호하는지를 c = 1 + α ⋅ r로 선형적으로 표현할 수 있다.
3-3. BPR Optimization with MF
선호도가 분명하게 드러나지 않는 Implicit Feedback에서 Ranking을 고려하여 서로 다른 아이템의 선호도를 반영한다. 유저 A가 item i보다 j를 더 선호한다면 이는 유저 A의 personalized ranking으로 이 정보를 MF의 파라미터에 학습에 이용한다.
Personalized Ranking은 아래 가정에 따르며 관측되지 않은 item에도 정보를 부여하여 학습하며 관측되지 않은 item에 대해서도 ranking이 가능하다는 특징이 있다.
[ 가정 ]
- 관측된 item > 관측되지 않은 item 선호
- 관측된 item끼리 선호도 추론 X
- 관측되지 않은 item끼리 선호도 추론 X
BPR 최적화는 최대 사후 확률 추정( Maximum A Posterior )에 따라 파라미터를 추정하여 이루어진다. 최적화는 LEARNBPR을 활용하는데 LEARNBPR은 Bootstrap 기반의 SGD를 사용하여 랜덤 샘플링 후 파라미터를 업데이트하는 방식이다.
참고할 논문 : https://www.google.com/url?sa=D&q=https://arxiv.org/pdf/1205.2618.pdf%3Fsource%3Dpost_page&ust=1626177840000000&usg=AOvVaw3rzSYKQ2yu3JpKyw2piAyt&hl=ko
3-4. Annoy
유저에게 추천하기 위해서는 벡터 연산이 필요한데 아이템 갯수가 많을수록 연산량이 많아져 실시간 서빙에 취약한다. Annoy는 이러한 문제를 해결하기 위한 알고리즘으로 주어진 벡터와 가장 유사한 벡터를 찾는다. 벡터 공간을 여러 구간을 나워 binary tree의 형태로 구성하여 주어진 벡터가 속한 공간을 tree search로 찾고, 해당 공간에서만 nearest neighbor 연산을 한다.

※ 강의노트는 러닝 스푼즈의 추천시스템 구현하기 수업을 듣고 정리한 내용이다.